Lecture 14 Gradient descent for more than one variable

14.1 Intution

Now we use gradient descent to optimize more than one variable. Let’s begin with two variable set up.

Consider the following function \[z = x^2 + 2y^2 + 2xy + 2x + 8y + 10\].
We first find the gradients \[f'_{x} = \frac{\partial z}{\partial x} = 2x + 2y + 2\] \[f'_{y} = \frac{\partial z}{\partial y} = 4y+2x+8\]
Now we want to use initial values for \(x_0 = 0\) and \(y_0 = 0\) and evaluate \[f'_{x} = 2x + 2y + 2 = 2(0)+2(0)+2 = 2\] \[f'_{y} = 4y+2x+8 = 4(0)+2(0)+8 = 8\]
Now we learn from these gradients by say, learning parameter of \(\alpha =0.1\) such that \[x_1 = x_0 - \alpha f'_{x} = 0 - 0.1(2) = -0.2\] \[y_1 = y_0 - \alpha f'_{y} = 0-0.1(8) = -0.8\]
Now we again use the updated value of \(x_1\) and \(y_1\), calculate the gradient \(f'_{x}\) and \(f'_{y}\), then learn from those gradients \(x_1 = x_0 - \alpha f'_{x}\) and \(y_1 = y_0 - \alpha f'_{y}\), until we converge to the solution.

14.2 Rcodes

Let me show you the R codes to do it.

This code defines a function called f that takes two arguments, x and y, and returns the value of the expression z that is defined within the function. The expression z is a quadratic function of x and y that has the form \(z = ax^2 + by^2 + cxy + dx + ey + f\), where a, b, c, d, e, and f are constants. In this particular case, the values of the constants are a = 1, b = 2, c = 2, d = 2, e = 8, and f = 10. This means that the function f will return the value of z for any given values of x and y that are passed to it as arguments

# define the function f(x, y)
f <- function(x, y) {
  # define the function
  z <- x^2 + 2*y^2 + 2 * x * y + 2 * x + 8 * y + 10
  # return the function value
  return(z)
}

For example, if we call the function f with arguments x = 2 and y = 3, it will return the value of z that corresponds to these values, which is \(z = 1 * 2^2 + 2 * 3^2 + 2 * 2 * 3 + 2 * 2 + 8 * 3 + 10 = 60\).

f(x = 2, y = 3)
#> [1] 72

Now lets define the gradients descent.

# define the gradient descent algorithm
gradient_descent <- function(x, y, learning_rate) {
  # calculate the gradient of f(x, y) with respect to x
  gradient_x <- 2 * x + 2 * y + 2
  # calculate the gradient of f(x, y) with respect to y
  gradient_y <- 4 * y + 2 * x + 8
  # update the value of x using the gradient and the learning rate
  x <- x - learning_rate * gradient_x
  # update the value of y using the gradient and the learning rate
  y <- y - learning_rate * gradient_y
  # return the updated values of x and y
  return(c(x, y))
}

This code defines a function called gradient_descent that implements the gradient descent algorithm for optimizing a function of two variables. The function takes three arguments: x, y, and learning_rate. The values of x and y are the starting values for the optimization, and the learning_rate is a parameter that controls the step size of the algorithm.

The function first calculates the gradient of the function f(x, y) with respect to x and y, using the formula for the partial derivative of a function. The gradient of a function tells us how the function changes as we vary its input values, and it is a useful quantity for optimization because it indicates the direction in which the function is increasing or decreasing. In this case, the gradient is calculated using the values of the constants in the definition of f(x, y) that were given in the previous answer.

Once the gradient has been calculated, the function updates the values of x and y using the gradient and the learning rate. This is the core step of the gradient descent algorithm, where we move in the direction of the gradient to find the minimum value of the function. The updated values of x and y are then returned by the function.

Now let’s initialize with x and y as zero with a learning rate of 0.1.

# set the initial values of x and y
x <- 0
y <- 0

# set the learning rate
learning_rate <- 0.1

The code first sets the initial values of x and y to 0. It then sets the learning rate, which is a parameter that controls the step size of the gradient descent algorithm. In this case, the learning rate is set to 0.1.

# run the gradient descent algorithm for 10 iterations
for (i in 1:500) {
  c <- gradient_descent(x, y, learning_rate)
  x <- c[1]
  y <- c[2]
  print(paste0(i, " ", x, " ", y))
}
#> [1] "1 -0.2 -0.8"
#> [1] "2 -0.2 -1.24"
#> [1] "3 -0.112 -1.504"
#> [1] "4 0.0112 -1.68"
#> [1] "5 0.14496 -1.81024"
#> [1] "6 0.278016 -1.915136"
#> [1] "7 0.40544 -2.0046848"
#> [1] "8 0.52528896 -2.08389888"
#> [1] "9 0.637010944 -2.15539712"
#> [1] "10 0.7406881792 -2.2206404608"
#> [1] "11 0.83667863552 -2.28052191232"
#> [1] "12 0.92544729088 -2.335648874496"
#> [1] "13 1.0074876076032 -2.3864787828736"
#> [1] "14 1.08328584265728 -2.4333847912448"
#> [1] "15 1.15330563237478 -2.47668804327834"
#> [1] "16 1.21798211455549 -2.51667395244196"
#> [1] "17 1.27772048213279 -2.55360079437627"
#> [1] "18 1.33289654458148 -2.58770457305232"
#> [1] "19 1.38385815027565 -2.61920205274769"
#> [1] "20 1.43092693077006 -2.64829286170374"
#> [1] "21 1.4744001169568 -2.67516110317626"
#> [1] "22 1.51455231420069 -2.69997668529711"
#> [1] "23 1.55163718841997 -2.72289647401841"
#> [1] "24 1.58588904553966 -2.74406532209504"
#> [1] "25 1.61752430085074 -2.76361700236496"
#> [1] "26 1.64674284115358 -2.78167506158912"
#> [1] "27 1.67372928524069 -2.79835360518419"
#> [1] "28 1.69865414922939 -2.81375802015865"
#> [1] "29 1.72167492341524 -2.82798564194107"
#> [1] "30 1.74293706712041 -2.84112636984769"
#> [1] "31 1.76257492766586 -2.85326323533269"
#> [1] "32 1.78071258919923 -2.86447292673279"
#> [1] "33 1.79746465670594 -2.87482627387952"
#> [1] "34 1.81293698014066 -2.8843886956689"
#> [1] "35 1.82722732324631 -2.89322061342947"
#> [1] "36 1.84042598128294 -2.90137783270694"
#> [1] "37 1.85261635156774 -2.90891189588075"
#> [1] "38 1.86387546043034 -2.915870407842"
#> [1] "39 1.87427444991267 -2.92229733679127"
#> [1] "40 1.88387902728839 -2.9282332920573"
#> [1] "41 1.89274988024217 -2.93371578069206"
#> [1] "42 1.90094306033215 -2.93877944446367"
#> [1] "43 1.90851033715845 -2.94345627874463"
#> [1] "44 1.91549952547569 -2.94777583467847"
#> [1] "45 1.92195478731625 -2.95176540590222"
#> [1] "46 1.92791691103344 -2.95545020100458"
#> [1] "47 1.93342356902767 -2.95885350280944"
#> [1] "48 1.93850955578402 -2.9619968154912"
#> [1] "49 1.94320700772546 -2.96490000045152"
#> [1] "50 1.94754560627067 -2.967581401816"
#> [1] "51 1.95155276537974 -2.97005796234374"
#> [1] "52 1.95525380477254 -2.97234533048219"
#> [1] "53 1.95867210991447 -2.97445795924382"
#> [1] "54 1.96182927978034 -2.97640919752919"
#> [1] "55 1.96474526333011 -2.97821137447358"
#> [1] "56 1.9674384855588 -2.97987587735017"
#> [1] "57 1.96992596391708 -2.98141322352186"
#> [1] "58 1.97222341583803 -2.98283312689653"
#> [1] "59 1.97434535804973 -2.98414455930553"
#> [1] "60 1.97630519830089 -2.98535580719326"
#> [1] "61 1.97811532007937 -2.98647452397614"
#> [1] "62 1.97978716085872 -2.98750777840155"
#> [1] "63 1.98133128436729 -2.98846209921268"
#> [1] "64 1.98275744733636 -2.98934351640106"
#> [1] "65 1.9840746611493 -2.99015759930791"
#> [1] "66 1.98529124878103 -2.99090949181461"
#> [1] "67 1.98641489738774 -2.99160394484497"
#> [1] "68 1.98745270687919 -2.99224534638453"
#> [1] "69 1.98841123478026 -2.99283774920656"
#> [1] "70 1.98929653766552 -2.99338489647998"
#> [1] "71 1.99011420942841 -2.99389024542109"
#> [1] "72 1.99086941662695 -2.99435698913834"
#> [1] "73 1.99156693112923 -2.99478807680839"
#> [1] "74 1.99221116026506 -2.99518623231088"
#> [1] "75 1.99280617467422 -2.99555397143954"
#> [1] "76 1.99335573402729 -2.99589361779857"
#> [1] "77 1.99386331078154 -2.9962073174846"
#> [1] "78 1.99433211212215 -2.99649705264707"
#> [1] "79 1.99476510022714 -2.99676465401267"
#> [1] "80 1.99516501098424 -2.99701181245303"
#> [1] "81 1.995534371278 -2.99724008966867"
#> [1] "82 1.99587551495613 -2.9974509280568"
#> [1] "83 1.99619059757627 -2.99764565982531"
#> [1] "84 1.99648161002608 -2.99782551541044"
#> [1] "85 1.99675039110295 -2.99799163125148"
#> [1] "86 1.99699863913265 -2.99814505697148"
#> [1] "87 1.99722792270042 -2.99828676200942"
#> [1] "88 1.99743969056222 -2.99841764174573"
#> [1] "89 1.99763528079892 -2.99853852315988"
#> [1] "90 1.99781592927111 -2.99865017005571"
#> [1] "91 1.99798277742803 -2.99875328788765"
#> [1] "92 1.99813687951996 -2.9988485282182"
#> [1] "93 1.99827920925961 -2.99893649283491"
#> [1] "94 1.99841066597467 -2.99901773755287"
#> [1] "95 1.99853208029031 -2.99909277572665"
#> [1] "96 1.99864421937758 -2.99916208149405"
#> [1] "97 1.99874779180087 -2.99922609277195"
#> [1] "98 1.99884345199509 -2.99928521402334"
#> [1] "99 1.99893180440074 -2.99933981881302"
#> [1] "100 1.99901340728319 -2.99939025216796"
#> [1] "101 1.99908877626015 -2.99943683275742"
#> [1] "102 1.9991583875596 -2.99947985490648"
#> [1] "103 1.99922268102898 -2.99951959045581"
#> [1] "104 1.99928206291434 -2.99955629047928"
#> [1] "105 1.99933690842733 -2.99959018687044"
#> [1] "106 1.99938756411595 -2.99962149380773"
#> [1] "107 1.99943435005431 -2.99965040910783"
#> [1] "108 1.99947756186501 -2.99967711547556"
#> [1] "109 1.99951747258712 -2.99970178165834"
#> [1] "110 1.99955433440136 -2.99972456351243"
#> [1] "111 1.99958838022358 -2.99974560498773"
#> [1] "112 1.99961982517641 -2.99976503903735"
#> [1] "113 1.9996488679486 -2.99978298845769"
#> [1] "114 1.99967569205042 -2.99979956666433"
#> [1] "115 1.9997004669732 -2.99981487840868"
#> [1] "116 1.9997233492603 -2.99982902043985"
#> [1] "117 1.99974448349621 -2.99984208211597"
#> [1] "118 1.99976400322016 -2.99985414596882"
#> [1] "119 1.99978203176989 -2.99986528822533"
#> [1] "120 1.99979868306098 -2.99987557928917"
#> [1] "121 1.99981406230662 -2.9998850841857"
#> [1] "122 1.99982826668243 -2.99989386297274"
#> [1] "123 1.9998413859405 -2.99990197112013"
#> [1] "124 1.99985350297642 -2.99990945986018"
#> [1] "125 1.99986469435317 -2.99991637651139"
#> [1] "126 1.99987503078482 -2.99992276477747"
#> [1] "127 1.99988457758335 -2.99992866502345"
#> [1] "128 1.99989339507137 -2.99993411453074"
#> [1] "129 1.99990153896324 -2.99993914773272"
#> [1] "130 1.99990906071714 -2.99994379643228"
#> [1] "131 1.99991600786016 -2.99994809000279"
#> [1] "132 1.99992242428869 -2.99995205557371"
#> [1] "133 1.99992835054569 -2.99995571820196"
#> [1] "134 1.99993382407695 -2.99995910103032"
#> [1] "135 1.99993887946762 -2.99996222543358"
#> [1] "136 1.99994354866081 -2.99996511115367"
#> [1] "137 1.99994786115939 -2.99996777642437"
#> [1] "138 1.99995184421238 -2.9999702380865"
#> [1] "139 1.9999555229872 -2.99997251169437"
#> [1] "140 1.99995892072864 -2.99997461161407"
#> [1] "141 1.99996205890572 -2.99997655111417"
#> [1] "142 1.99996495734741 -2.99997834244965"
#> [1] "143 1.99996763436786 -2.99997999693927"
#> [1] "144 1.99997010688214 -2.99998152503713"
#> [1] "145 1.99997239051314 -2.99998293639871"
#> [1] "146 1.99997449969025 -2.99998423994185"
#> [1] "147 1.99997644774057 -2.99998544390316"
#> [1] "148 1.99997824697309 -2.99998655589001"
#> [1] "149 1.99997990875648 -2.99998758292863"
#> [1] "150 1.99998144359091 -2.99998853150847"
#> [1] "151 1.99998286117442 -2.99998940762326"
#> [1] "152 1.99998417046419 -2.99999021680884"
#> [1] "153 1.99998537973312 -2.99999096417814"
#> [1] "154 1.99998649662212 -2.99999165445351"
#> [1] "155 1.9999875281884 -2.99999229199653"
#> [1] "156 1.99998848095003 -2.9999928808356"
#> [1] "157 1.99998936092714 -2.99999342469136"
#> [1] "158 1.99999017367999 -2.99999392700025"
#> [1] "159 1.99999092434404 -2.99999439093615"
#> [1] "160 1.99999161766246 -2.99999481943049"
#> [1] "161 1.99999225801607 -2.99999521519079"
#> [1] "162 1.99999284945101 -2.99999558071769"
#> [1] "163 1.99999339570435 -2.99999591832081"
#> [1] "164 1.99999390022764 -2.99999623013336"
#> [1] "165 1.99999436620878 -2.99999651812554"
#> [1] "166 1.99999479659213 -2.99999678411708"
#> [1] "167 1.99999519409712 -2.99999702978868"
#> [1] "168 1.99999556123543 -2.99999725669263"
#> [1] "169 1.99999590032687 -2.99999746626266"
#> [1] "170 1.99999621351403 -2.99999765982297"
#> [1] "171 1.99999650277582 -2.99999783859659"
#> [1] "172 1.99999676993997 -2.99999800371312"
#> [1] "173 1.9999970166946 -2.99999815621587"
#> [1] "174 1.99999724459886 -2.99999829706844"
#> [1] "175 1.99999745509277 -2.99999842716084"
#> [1] "176 1.99999764950639 -2.99999854731506"
#> [1] "177 1.99999782906812 -2.99999865829031"
#> [1] "178 1.99999799491256 -2.99999876078781"
#> [1] "179 1.99999814808761 -2.9999988554552"
#> [1] "180 1.99999828956113 -2.99999894289064"
#> [1] "181 1.99999842022703 -2.99999902364661"
#> [1] "182 1.99999854091094 -2.99999909823337"
#> [1] "183 1.99999865237543 -2.99999916712221"
#> [1] "184 1.99999875532479 -2.99999923074841"
#> [1] "185 1.99999885040951 -2.99999928951401"
#> [1] "186 1.99999893823041 -2.99999934379031"
#> [1] "187 1.99999901934239 -2.99999939392027"
#> [1] "188 1.99999909425796 -2.99999944022064"
#> [1] "189 1.9999991634505 -2.99999948298398"
#> [1] "190 1.99999922735719 -2.99999952248048"
#> [1] "191 1.99999928638185 -2.99999955895973"
#> [1] "192 1.99999934089743 -2.99999959265221"
#> [1] "193 1.99999939124838 -2.99999962377081"
#> [1] "194 1.99999943775287 -2.99999965251216"
#> [1] "195 1.99999948070473 -2.99999967905787"
#> [1] "196 1.99999952037536 -2.99999970357567"
#> [1] "197 1.99999955701542 -2.99999972622047"
#> [1] "198 1.99999959085643 -2.99999974713537"
#> [1] "199 1.99999962211222 -2.99999976645251"
#> [1] "200 1.99999965098028 -2.99999978429395"
#> [1] "201 1.99999967764301 -2.99999980077242"
#> [1] "202 1.99999970226889 -2.99999981599206"
#> [1] "203 1.99999972501353 -2.99999983004901"
#> [1] "204 1.99999974602062 -2.99999984303211"
#> [1] "205 1.99999976542292 -2.99999985502339"
#> [1] "206 1.99999978334301 -2.99999986609862"
#> [1] "207 1.99999979989414 -2.99999987632777"
#> [1] "208 1.99999981518086 -2.99999988577549"
#> [1] "209 1.99999982929979 -2.99999989450147"
#> [1] "210 1.99999984234012 -2.99999990256084"
#> [1] "211 1.99999985438427 -2.99999991000453"
#> [1] "212 1.99999986550832 -2.99999991687957"
#> [1] "213 1.99999987578257 -2.99999992322941"
#> [1] "214 1.99999988527194 -2.99999992909416"
#> [1] "215 1.99999989403638 -2.99999993451088"
#> [1] "216 1.99999990213128 -2.99999993951381"
#> [1] "217 1.99999990960779 -2.99999994413454"
#> [1] "218 1.99999991651314 -2.99999994840228"
#> [1] "219 1.99999992289097 -2.999999952344"
#> [1] "220 1.99999992878157 -2.99999995598459"
#> [1] "221 1.99999993422218 -2.99999995934707"
#> [1] "222 1.99999993924715 -2.99999996245268"
#> [1] "223 1.99999994388826 -2.99999996532104"
#> [1] "224 1.99999994817481 -2.99999996797027"
#> [1] "225 1.99999995213391 -2.99999997041713"
#> [1] "226 1.99999995579055 -2.99999997267706"
#> [1] "227 1.99999995916785 -2.99999997476434"
#> [1] "228 1.99999996228715 -2.99999997669218"
#> [1] "229 1.99999996516816 -2.99999997847274"
#> [1] "230 1.99999996782907 -2.99999998011727"
#> [1] "231 1.99999997028671 -2.99999998163618"
#> [1] "232 1.99999997255661 -2.99999998303905"
#> [1] "233 1.99999997465309 -2.99999998433475"
#> [1] "234 1.99999997658943 -2.99999998553147"
#> [1] "235 1.99999997837783 -2.99999998663677"
#> [1] "236 1.99999998002962 -2.99999998765763"
#> [1] "237 1.99999998155522 -2.9999999886005"
#> [1] "238 1.99999998296428 -2.99999998947134"
#> [1] "239 1.99999998426569 -2.99999999027566"
#> [1] "240 1.99999998546769 -2.99999999101854"
#> [1] "241 1.99999998657786 -2.99999999170466"
#> [1] "242 1.99999998760322 -2.99999999233837"
#> [1] "243 1.99999998855025 -2.99999999292366"
#> [1] "244 1.99999998942493 -2.99999999346425"
#> [1] "245 1.99999999023279 -2.99999999396353"
#> [1] "246 1.99999999097894 -2.99999999442468"
#> [1] "247 1.99999999166809 -2.9999999948506"
#> [1] "248 1.99999999230459 -2.99999999524398"
#> [1] "249 1.99999999289247 -2.9999999956073"
#> [1] "250 1.99999999343543 -2.99999999594288"
#> [1] "251 1.99999999393692 -2.99999999625281"
#> [1] "252 1.9999999944001 -2.99999999653907"
#> [1] "253 1.99999999482789 -2.99999999680346"
#> [1] "254 1.99999999522301 -2.99999999704766"
#> [1] "255 1.99999999558794 -2.9999999972732"
#> [1] "256 1.99999999592499 -2.99999999748151"
#> [1] "257 1.99999999623629 -2.9999999976739"
#> [1] "258 1.99999999652381 -2.9999999978516"
#> [1] "259 1.99999999678937 -2.99999999801572"
#> [1] "260 1.99999999703464 -2.99999999816731"
#> [1] "261 1.99999999726117 -2.99999999830731"
#> [1] "262 1.9999999974704 -2.99999999843662"
#> [1] "263 1.99999999766365 -2.99999999855605"
#> [1] "264 1.99999999784213 -2.99999999866636"
#> [1] "265 1.99999999800697 -2.99999999876824"
#> [1] "266 1.99999999815923 -2.99999999886234"
#> [1] "267 1.99999999829985 -2.99999999894925"
#> [1] "268 1.99999999842973 -2.99999999902952"
#> [1] "269 1.99999999854969 -2.99999999910366"
#> [1] "270 1.99999999866048 -2.99999999917213"
#> [1] "271 1.99999999876281 -2.99999999923538"
#> [1] "272 1.99999999885733 -2.99999999929379"
#> [1] "273 1.99999999894462 -2.99999999934774"
#> [1] "274 1.99999999902524 -2.99999999939757"
#> [1] "275 1.99999999909971 -2.99999999944359"
#> [1] "276 1.99999999916848 -2.99999999948609"
#> [1] "277 1.99999999923201 -2.99999999952535"
#> [1] "278 1.99999999929067 -2.99999999956161"
#> [1] "279 1.99999999934486 -2.9999999995951"
#> [1] "280 1.99999999939491 -2.99999999962603"
#> [1] "281 1.99999999944114 -2.9999999996546"
#> [1] "282 1.99999999948383 -2.99999999968099"
#> [1] "283 1.99999999952326 -2.99999999970536"
#> [1] "284 1.99999999955968 -2.99999999972787"
#> [1] "285 1.99999999959332 -2.99999999974866"
#> [1] "286 1.99999999962439 -2.99999999976786"
#> [1] "287 1.99999999965308 -2.99999999978559"
#> [1] "288 1.99999999967958 -2.99999999980197"
#> [1] "289 1.99999999970406 -2.9999999998171"
#> [1] "290 1.99999999972667 -2.99999999983107"
#> [1] "291 1.99999999974755 -2.99999999984398"
#> [1] "292 1.99999999976683 -2.9999999998559"
#> [1] "293 1.99999999978465 -2.9999999998669"
#> [1] "294 1.9999999998011 -2.99999999987707"
#> [1] "295 1.99999999981629 -2.99999999988646"
#> [1] "296 1.99999999983033 -2.99999999989514"
#> [1] "297 1.99999999984329 -2.99999999990315"
#> [1] "298 1.99999999985526 -2.99999999991055"
#> [1] "299 1.99999999986632 -2.99999999991738"
#> [1] "300 1.99999999987653 -2.99999999992369"
#> [1] "301 1.99999999988596 -2.99999999992952"
#> [1] "302 1.99999999989467 -2.9999999999349"
#> [1] "303 1.99999999990272 -2.99999999993988"
#> [1] "304 1.99999999991015 -2.99999999994447"
#> [1] "305 1.99999999991702 -2.99999999994871"
#> [1] "306 1.99999999992335 -2.99999999995263"
#> [1] "307 1.99999999992921 -2.99999999995625"
#> [1] "308 1.99999999993462 -2.99999999995959"
#> [1] "309 1.99999999993961 -2.99999999996268"
#> [1] "310 1.99999999994423 -2.99999999996553"
#> [1] "311 1.99999999994849 -2.99999999996816"
#> [1] "312 1.99999999995242 -2.9999999999706"
#> [1] "313 1.99999999995606 -2.99999999997284"
#> [1] "314 1.99999999995941 -2.99999999997492"
#> [1] "315 1.99999999996251 -2.99999999997683"
#> [1] "316 1.99999999996538 -2.9999999999786"
#> [1] "317 1.99999999996802 -2.99999999998024"
#> [1] "318 1.99999999997047 -2.99999999998175"
#> [1] "319 1.99999999997272 -2.99999999998314"
#> [1] "320 1.99999999997481 -2.99999999998443"
#> [1] "321 1.99999999997673 -2.99999999998562"
#> [1] "322 1.99999999997851 -2.99999999998672"
#> [1] "323 1.99999999998015 -2.99999999998773"
#> [1] "324 1.99999999998167 -2.99999999998867"
#> [1] "325 1.99999999998307 -2.99999999998953"
#> [1] "326 1.99999999998436 -2.99999999999033"
#> [1] "327 1.99999999998556 -2.99999999999107"
#> [1] "328 1.99999999998666 -2.99999999999175"
#> [1] "329 1.99999999998768 -2.99999999999238"
#> [1] "330 1.99999999998862 -2.99999999999297"
#> [1] "331 1.99999999998949 -2.9999999999935"
#> [1] "332 1.99999999999029 -2.999999999994"
#> [1] "333 1.99999999999103 -2.99999999999446"
#> [1] "334 1.99999999999172 -2.99999999999488"
#> [1] "335 1.99999999999235 -2.99999999999527"
#> [1] "336 1.99999999999293 -2.99999999999563"
#> [1] "337 1.99999999999347 -2.99999999999597"
#> [1] "338 1.99999999999397 -2.99999999999627"
#> [1] "339 1.99999999999443 -2.99999999999656"
#> [1] "340 1.99999999999486 -2.99999999999682"
#> [1] "341 1.99999999999525 -2.99999999999707"
#> [1] "342 1.99999999999561 -2.99999999999729"
#> [1] "343 1.99999999999595 -2.9999999999975"
#> [1] "344 1.99999999999626 -2.99999999999769"
#> [1] "345 1.99999999999654 -2.99999999999786"
#> [1] "346 1.99999999999681 -2.99999999999803"
#> [1] "347 1.99999999999705 -2.99999999999818"
#> [1] "348 1.99999999999728 -2.99999999999832"
#> [1] "349 1.99999999999749 -2.99999999999845"
#> [1] "350 1.99999999999768 -2.99999999999856"
#> [1] "351 1.99999999999785 -2.99999999999867"
#> [1] "352 1.99999999999802 -2.99999999999878"
#> [1] "353 1.99999999999817 -2.99999999999887"
#> [1] "354 1.99999999999831 -2.99999999999896"
#> [1] "355 1.99999999999844 -2.99999999999904"
#> [1] "356 1.99999999999856 -2.99999999999911"
#> [1] "357 1.99999999999867 -2.99999999999918"
#> [1] "358 1.99999999999877 -2.99999999999924"
#> [1] "359 1.99999999999886 -2.9999999999993"
#> [1] "360 1.99999999999895 -2.99999999999935"
#> [1] "361 1.99999999999903 -2.9999999999994"
#> [1] "362 1.99999999999911 -2.99999999999945"
#> [1] "363 1.99999999999917 -2.99999999999949"
#> [1] "364 1.99999999999924 -2.99999999999953"
#> [1] "365 1.9999999999993 -2.99999999999956"
#> [1] "366 1.99999999999935 -2.9999999999996"
#> [1] "367 1.9999999999994 -2.99999999999963"
#> [1] "368 1.99999999999944 -2.99999999999966"
#> [1] "369 1.99999999999949 -2.99999999999968"
#> [1] "370 1.99999999999953 -2.99999999999971"
#> [1] "371 1.99999999999956 -2.99999999999973"
#> [1] "372 1.9999999999996 -2.99999999999975"
#> [1] "373 1.99999999999963 -2.99999999999977"
#> [1] "374 1.99999999999966 -2.99999999999979"
#> [1] "375 1.99999999999968 -2.9999999999998"
#> [1] "376 1.99999999999971 -2.99999999999982"
#> [1] "377 1.99999999999973 -2.99999999999983"
#> [1] "378 1.99999999999975 -2.99999999999985"
#> [1] "379 1.99999999999977 -2.99999999999986"
#> [1] "380 1.99999999999979 -2.99999999999987"
#> [1] "381 1.9999999999998 -2.99999999999988"
#> [1] "382 1.99999999999982 -2.99999999999989"
#> [1] "383 1.99999999999983 -2.9999999999999"
#> [1] "384 1.99999999999984 -2.9999999999999"
#> [1] "385 1.99999999999986 -2.99999999999991"
#> [1] "386 1.99999999999987 -2.99999999999992"
#> [1] "387 1.99999999999988 -2.99999999999992"
#> [1] "388 1.99999999999989 -2.99999999999993"
#> [1] "389 1.9999999999999 -2.99999999999994"
#> [1] "390 1.9999999999999 -2.99999999999994"
#> [1] "391 1.99999999999991 -2.99999999999994"
#> [1] "392 1.99999999999992 -2.99999999999995"
#> [1] "393 1.99999999999992 -2.99999999999995"
#> [1] "394 1.99999999999993 -2.99999999999996"
#> [1] "395 1.99999999999993 -2.99999999999996"
#> [1] "396 1.99999999999994 -2.99999999999996"
#> [1] "397 1.99999999999994 -2.99999999999997"
#> [1] "398 1.99999999999995 -2.99999999999997"
#> [1] "399 1.99999999999995 -2.99999999999997"
#> [1] "400 1.99999999999996 -2.99999999999997"
#> [1] "401 1.99999999999996 -2.99999999999998"
#> [1] "402 1.99999999999996 -2.99999999999998"
#> [1] "403 1.99999999999997 -2.99999999999998"
#> [1] "404 1.99999999999997 -2.99999999999998"
#> [1] "405 1.99999999999997 -2.99999999999998"
#> [1] "406 1.99999999999997 -2.99999999999998"
#> [1] "407 1.99999999999997 -2.99999999999998"
#> [1] "408 1.99999999999998 -2.99999999999999"
#> [1] "409 1.99999999999998 -2.99999999999999"
#> [1] "410 1.99999999999998 -2.99999999999999"
#> [1] "411 1.99999999999998 -2.99999999999999"
#> [1] "412 1.99999999999998 -2.99999999999999"
#> [1] "413 1.99999999999998 -2.99999999999999"
#> [1] "414 1.99999999999999 -2.99999999999999"
#> [1] "415 1.99999999999999 -2.99999999999999"
#> [1] "416 1.99999999999999 -2.99999999999999"
#> [1] "417 1.99999999999999 -2.99999999999999"
#> [1] "418 1.99999999999999 -2.99999999999999"
#> [1] "419 1.99999999999999 -2.99999999999999"
#> [1] "420 1.99999999999999 -2.99999999999999"
#> [1] "421 1.99999999999999 -2.99999999999999"
#> [1] "422 1.99999999999999 -3"
#> [1] "423 1.99999999999999 -3"
#> [1] "424 1.99999999999999 -3"
#> [1] "425 1.99999999999999 -3"
#> [1] "426 1.99999999999999 -3"
#> [1] "427 1.99999999999999 -3"
#> [1] "428 2 -3"
#> [1] "429 2 -3"
#> [1] "430 2 -3"
#> [1] "431 2 -3"
#> [1] "432 2 -3"
#> [1] "433 2 -3"
#> [1] "434 2 -3"
#> [1] "435 2 -3"
#> [1] "436 2 -3"
#> [1] "437 2 -3"
#> [1] "438 2 -3"
#> [1] "439 2 -3"
#> [1] "440 2 -3"
#> [1] "441 2 -3"
#> [1] "442 2 -3"
#> [1] "443 2 -3"
#> [1] "444 2 -3"
#> [1] "445 2 -3"
#> [1] "446 2 -3"
#> [1] "447 2 -3"
#> [1] "448 2 -3"
#> [1] "449 2 -3"
#> [1] "450 2 -3"
#> [1] "451 2 -3"
#> [1] "452 2 -3"
#> [1] "453 2 -3"
#> [1] "454 2 -3"
#> [1] "455 2 -3"
#> [1] "456 2 -3"
#> [1] "457 2 -3"
#> [1] "458 2 -3"
#> [1] "459 2 -3"
#> [1] "460 2 -3"
#> [1] "461 2 -3"
#> [1] "462 2 -3"
#> [1] "463 2 -3"
#> [1] "464 2 -3"
#> [1] "465 2 -3"
#> [1] "466 2 -3"
#> [1] "467 2 -3"
#> [1] "468 2 -3"
#> [1] "469 2 -3"
#> [1] "470 2 -3"
#> [1] "471 2 -3"
#> [1] "472 2 -3"
#> [1] "473 2 -3"
#> [1] "474 2 -3"
#> [1] "475 2 -3"
#> [1] "476 2 -3"
#> [1] "477 2 -3"
#> [1] "478 2 -3"
#> [1] "479 2 -3"
#> [1] "480 2 -3"
#> [1] "481 2 -3"
#> [1] "482 2 -3"
#> [1] "483 2 -3"
#> [1] "484 2 -3"
#> [1] "485 2 -3"
#> [1] "486 2 -3"
#> [1] "487 2 -3"
#> [1] "488 2 -3"
#> [1] "489 2 -3"
#> [1] "490 2 -3"
#> [1] "491 2 -3"
#> [1] "492 2 -3"
#> [1] "493 2 -3"
#> [1] "494 2 -3"
#> [1] "495 2 -3"
#> [1] "496 2 -3"
#> [1] "497 2 -3"
#> [1] "498 2 -3"
#> [1] "499 2 -3"
#> [1] "500 2 -3"

This code uses the gradient_descent function that was defined previously to answer to find the minimum value of the function f(x, y). It does this by running the gradient descent algorithm for a fixed number of iterations, say 500 iterations, starting from initial values of x and y that are set at the beginning of the code.

The code runs the gradient descent algorithm for 500 iterations. This is done using a for loop that calls the gradient_descent function on each iteration, passing in the current values of x and y as arguments. The gradient_descent function returns the updated values of x and y, which are then assigned to the variables x and y in the loop.

After each iteration, the code prints the iteration number, the value of x, and the value of y to the console. This allows us to see how the values of x and y change over the course of the optimization.

For the given function \(z = x^2 + 2y^2 + 2xy + 2x + 8y + 10\), the value of \(x\) as 2 and \(y\) as -3 minimizes the function. The minimum value of the function is zero.

f(x = x, y = y)
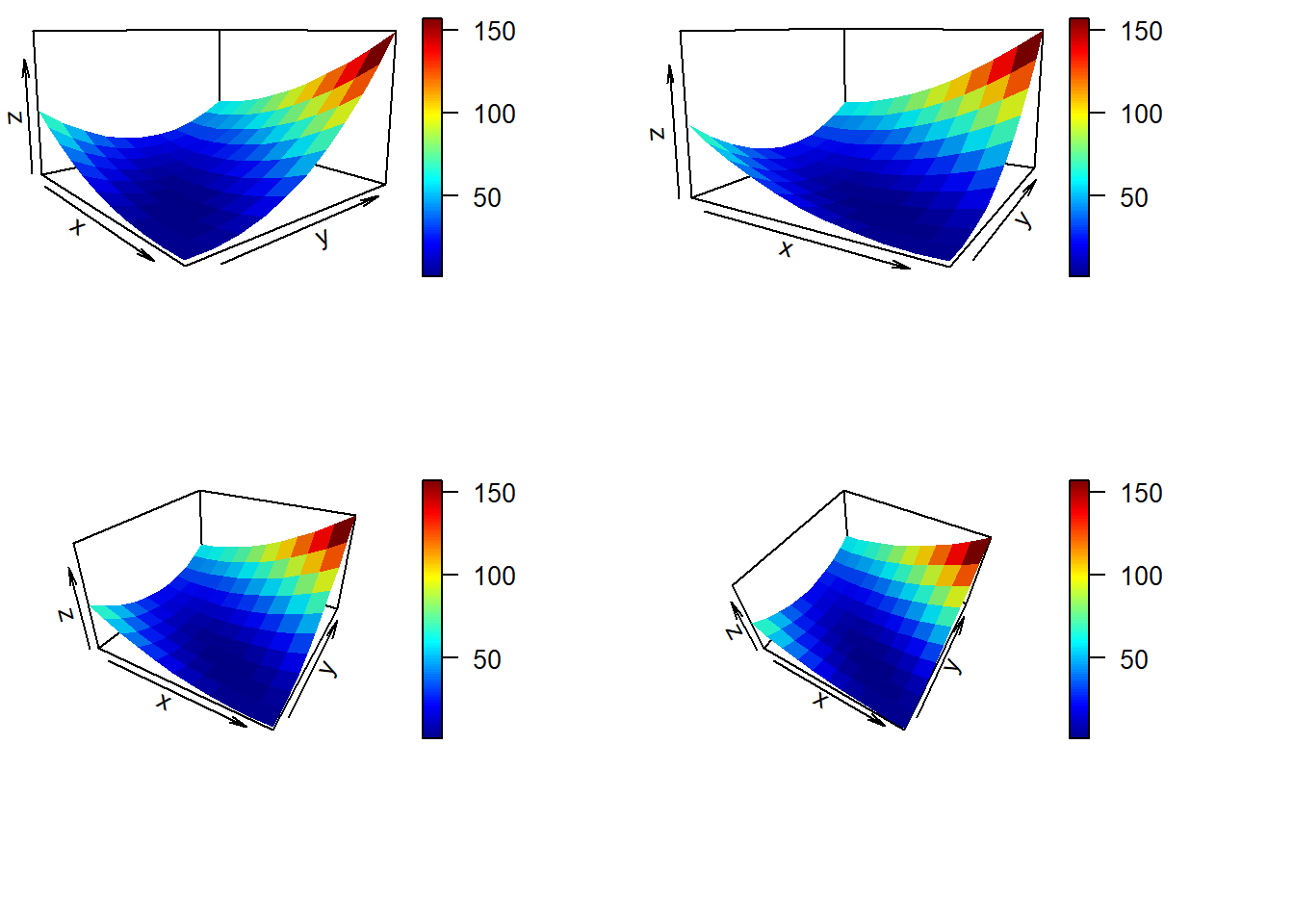
#> [1] 1.776357e-15

Let’s plot the function.

xaxis <- -5:5
yaxis <- -5:5
zaxis <- outer(xaxis, yaxis, f)
library(plot3D)
#> Warning: package 'plot3D' was built under R version 4.0.5
par(mfrow = c(2, 2), mai = c(1, 0.1, 0.1, 1))
persp3D(z = zaxis, x = xaxis, y = yaxis, 
        phi = 10, 
        theta = 50, 
        box = TRUE, border = NA, shade = .1, expand = 0.6, contour = F)

persp3D(z = zaxis, x = xaxis, y = yaxis, 
        phi = 10, 
        theta = 30, 
        box = TRUE, border = NA, shade = .1, expand = 0.6, contour = F)

persp3D(z = zaxis, x = xaxis, y = yaxis, 
        phi = 30, 
        theta = 30, 
        box = TRUE, border = NA, shade = .1, expand = 0.6, contour = F)

persp3D(z = zaxis, x = xaxis, y = yaxis, 
        phi = 50, 
        theta = 30, 
        box = TRUE, border = NA, shade = .1, expand = 0.6, contour = F)

par(mfrow = c(1, 1))

14.3 Exercise

E1. Update the above codes using while statement.

13 Gradient descent

15 Gradient descent for simple regression